About Us Services Resources Contact SMD Discuss
|
|||||||||||||
Approaches to Segmentation
©2009 Scott Davis and Strategic Marketing Decisions. Any distribution or other commercial use of the contents of this website is prohibited unless written permission is obtained from Scott Davis and Strategic Marketing Decisions.
|
|||||||||||||
| Table 1. Common Segmentation Criteria | |
Consumer Markets |
Business Markets |
Demographic factors: age, gender, marital status, family size and composition, occupation, income, education, ethnic background, religion |
Demographic factors: industry, company size (unit volume, number of employees, etc.), profit status (profit versus nonprofit), financial resources or performance, number of facilities under management |
Geographic factors: region, community type (urban, suburban, rural), climate |
Geographic factors: region or country, community type (urban, suburban, rural), population, cost of living, average education or skill level |
Product preference and use: purchase size and frequency (usage rate), feature preference, brand loyalty, price sensitivity, usage occasions, product knowledge or experience |
Product preference and use: purchase size and frequency (usage rate), feature preference, brand or vendor loyalty, price sensitivity, risk aversion, product use, product knowledge or experience |
Psychographic: social class, personality, lifestyle (beliefs and activities participating in) |
Purchasing structure and process: management structure, are budget process, allocation of purchase decision authority, role of the user in the purchase decisions, purchase process |
Customers may vary in their attitudes about products in a number of ways. They may have different beliefs regarding which products are available, the features of those products, and the ability of various products to satisfy their needs and desires. They may also have different priorities are preferences for product features and sensitivity to price. For example, in the market for personal computers, gamers value highly functional graphics and audio cards and are willing to pay a premium for them. Business users such as data analysts will be interested in CPU speed and will pay for that capability but are less sensitive to video performance. They will tend to be more concerned with getting a good value for their investment. By contrast many senior citizens are primarily interested in computers that allow them to get their electronic mail and will be more sensitive to price.
They may also vary in how they make purchase decisions. One reason is differences in how they use information. Some customers may systematically process information concerning the product features and how important they are and try to optimize. These customers will tend to make a purchase decision based on which alternative they believe will give them the greatest benefits or utility per dollar spent. In contrast, other customers may simply make choices based on habit, impulse or rules of thumb. Fore example, brand loyal customers may continue to choose their preferred brand as long as price is deemed acceptable while deal prone customers may simply choose the brand offering the best price discount in absolute or percentage terms.
Customers may also differ in terms of who makes the purchase decision. When the decision maker is also the person will use the product much more attention is paid to the product’s performance; whereas, a decision maker whose priority is managing a budget will pay much more attention to the product's price. This is particularly important in business-to-business markets in which multiple parties often have an impact on the choice decision. A customer’s vendor choice may also influence the choice of products available as well as the information they can receive a bout the alternatives.
Market segments will generally differ in terms of their potential for sales volume and profitability. Price-sensitive customers are going to be more likely to search out competitive offers and choosing an alternative of acceptable quality that has the lowest price. The profit potential of the segments will tend to be small unless the seller has a cost advantage or the sales volume potential is sufficiently large to compensate for a small contribution per unit or generate scale economies. Customers may also differ in the cost of serving them. In the insurance industry there are systematic variations across customer types in terms of both the likelihood and cost of claims filed. Most insurance companies employ systematic actuarial analyses in setting both their offerings and rates, with different rates being charged to customers having different characteristics. For example auto insurers will charge higher rates to younger drivers because of historical evidence that indicates the drivers in that age group have higher accident rates.
QUALITATIVE SEGMENTATION TECHNIQUES
Markets can be segmented using judgment based on qualitative observations and a statistical analysis of available data. Qualitative approaches draw on the assessment by sales representatives or management of how purchase behavior varies with customer characteristics. Many valuable insights can be derived by sales representatives who may observe that different customer types common display patterns in preferences and the ways decisions are made or objections to purchase.
A key to the success of a qualitative segmentation approach is a systematically gathering and processing information about current and potential customers. This data may come simply from direct interactions with customers or may be augmented by market research studies such as surveys and focus groups. Useful information to gather includes how they use the product, which alternatives they consider and how they evaluate their effectiveness in meeting their needs, how they make purchase decisions, and how much they value differentiating features. By observing common themes in customer responses, it may be possible to identify how different customer types vary in the offerings they consider and how they value competing alternatives. Systematically collecting data can be a very valuable tool when using judgment to segment a market and reduces the reliance on pure intuition.
CROSS TABULAR ANALYSIS
Systematically collecting data may also make it possible to employ quantitative tools to assist in segmenting a market. In segmenting a market it is useful to examine how variables relating to a segment’s attractiveness (such as preference, current purchase likelihood, average purchase size, average customer expenditures in the category, expected cost of service, etc.) vary with variables that could be used to define a segment. A cross tabular analysis can be a useful tool to examine the interrelationships between categorical variables describing segments’ characteristics and their potential attractiveness.
A cross tabular analysis begins by defining categories for the variables to be considered. In defining categories, variables should be fully inclusive in that all observations should fall into one category and mutually exclusive so that no one observation should fall into more than one category. In many cases this may be straightforward as is the case with gender. Often, however, variables cannot be described in such an obvious way. Categories for continuous variables, such as age or income, must be subjectively defined based on the analyst’s judgment. Once the categories are defined, a table is created that summarizes how frequently an observation from one category occurs in another category.
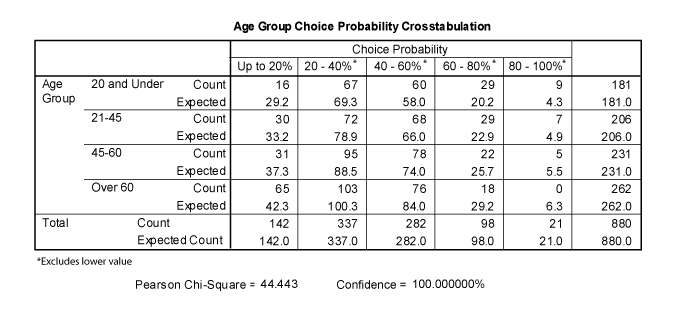
Consider the example of a customer panel that describes the frequency of purchase of a soft drink called Fizz Cola. In this example a group of 880 consumers monitored their soft drink consumption for a period of three months. In this panel demographic data was collected as well as a purchase history for each participant. One potential segmentation criterion for this market was age. Age could be a meaningful basis for segmentation if brand preference varied systematically by age. To begin the analysis, each respondent was placed in an age category that was defined by the analyst. Brand choice probabilities also were divided into five categories to describe brand preference or loyalty. Those who chose Fizz less than twenty percent of the time could be viewed as preferring another brand while those choosing Fizz more than 80 percent of the time could be viewed as relatively brand loyal.
The survey results are summarized in Table 2. Each cell contains the count of participants in each age group with a given choice probability. If brand choice probability was uninfluenced by age then one would expect the entries in each cell to be close to the expected number of entries in the cell that would occur if the observations were allocated to cells randomly based on how frequently each category occurred in the entire set of observations. In the example, the expected number of cases of those under 21 choosing Fizz less than 20 percent of the time would be the proportion of panel members under 21 (181/880) times the proportion of the panel members choosing Fizz less than 20 percent of the time (142/880) times the number of panel members (880), which would be 29.2. Since the actual number of observations in that cell is 16, we might conclude that young people are less likely to prefer another brand than the population as a whole.
Table 2. Crosstabulation for soft drink consumers
The significance of a classification scheme can be assessed by the degree to which the entries in each cell differ from the values that would occur if the variables were independent. Pearson Chi-Squared statistic provides a measure of how likely it is that the two categorical variables are independent. It is computed using the formula:
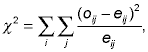
Where oij is the observed number of observations in the cell row i and column j and eij is the number or observations that would be expected if the row variable and column variable were independent. This value is large if the observed values differ from the values that would be expected with independence. To determine whether this value is statistically significant it should be interpreted in terms of the number of rows and columns in the table. The degrees of freedom for this statistic are given by the number of rows minus one times the number of columns minus one, or (r-1)×(c-1). For the panel in this example the Chi-Squared statistic is 44.4 and there are (5-1)×(4-1), or 12 degrees of freedom. If age and choice probability were unrelated, this value would occur less than .5 percent of the time when there are 12 degrees of freedom .
To interpret the table, it appears that young consumers are much more likely to purchase Fizz than the population as a whole and that older adults are more likely to choose another brand. This analysis does not explain why the different age groups chose the way they did. Differences could be due to differences in brand preference, but could also be due to differences in sensitivity to other marketing variables such as price, price promotion frequency, or the availability of the product at certain purchase locations. As such, it would be valuable to examine consumer perceptions, preferences and buying behavior in more depth. However, it would usually be a mistake to aggregate findings on these dimensions across segments.
In this example it appears that age may be a useful criterion in segmenting the market since the choices of different age groups differ significantly from one another. However, age may be one of several criteria that can be used in explaining differences in soft drink choice in this example. Similar cross-tabulation tables could be constructed examining the covariation of other variables that could explain variations in choice likelihood, such a gender, family or neighborhood income, lifestyle variables (such as participation in sports or other social activities), and the like. There will often be multiple measures of a segment’s attractiveness or a brand’s effectiveness in serving it. This example looked at choice probability but it may also make sense to consider other performance variables such as the number of units sold per customer or profits per customer. A segmentation scheme will be more useful when the segmentation criteria provide a significant explanation of multiple measures of segment attractiveness or brand performance.
INTERACTION DETECTION ANALYSIS
When there are many variables that could provide possible segmentation criteria, it can be challenging to integrate them into a unified segmentation scheme using a cross tabular analysis. Interaction detection approaches can be used to consider how a set of explanatory variables can be used to form segments that explain variations in a specified dependent variable. As such, these approaches provide a methodology for integrating and prioritizing statistical insights that could be obtained by a set of cross-tabular analyses.
CHAID (Chi-squared Automated Interaction Detection) is a widely used technique that selects explanatory variables based on a Chi-squared test between the categories of these variables and the categories of the specified dependent variable. For each potential explanatory variable, a Chi-squared statistic is computed for each set of categories of it and the dependent variable. The algorithm typically chooses the explanatory variable with the largest Chi-squared statistic as the first basis for forming subgroups from the total population. Once this split occurs, the analysis can be repeated for each of the subgroups to determine if any of the explanatory variables can statistically significantly form additional subgroups from the population of each of the previously formed subgroups. The process continues until either there are no more significant splits possible or the user terminates the process. The result is a “tree” in which the trunk node is comprised of the entire population and the nodes defined by each of the branches represent the part of the population that falls within the defined segment.
To illustrate, we return to the example of the Fizz Cola panel data. As in the cross tabular analysis, we are attempting to define a segmentation scheme that explains variations in the dependent variable, brand choice probability. A set of five potential explanatory variables was tested: age, gender, marital status, an indicator of physical activity (how frequently they participate in an individual or team sport), and an indicator of social activity (how frequently they get together with non-family members for social activities other than sports). The CHAID analysis findings are summarized in Figure 1.
Figure 1. CHAID Classification Tree
The algorithm determined that age was the most significant variable in explaining variations in choice probability. As in the cross tabular analysis, younger people were more likely to choose Fizz than older adults. In contrast to the cross tabular analysis, it determined that explanatory power was stronger when the adults in the age group from 21 to 60 were combined into a single category. The explanatory variables were tested to see if any of them could provide a significant explanation of the variation within each of the three age-defined subcategories. The CHAID analysis determined that variation in choice probability among those under twenty and those over 60 could be significantly explained by gender, with males being more likely to choose Fizz. It also determined that the variation in choice probability among adults in the 21-60 age group could be best explained by marital status, with those who are married being more likely to choose Fizz. The end result is a set of six segments that are defined by a combination of age, gender and marital status.
In this example brand choice likelihood was the only measure of segment performance/attractiveness considered in statistically forming a segmentation scheme. To be confident that this scheme is the most appropriate, it would be useful to consider other measures to see if a similar pattern occurred. In this example, a measure of usage intensity (e.g. number units purchased per week or month) or category expenditures would also be valuable dependent variables in determining differences in buying behavior. One could have great confidence in the segmentation scheme if a similar segmentation scheme arose from a CHAID analysis of those other variables.
CLUSTERING METHODS
Cross tabular and interaction detection analysis are procedures that are used to segment the market by identifying criteria that can be used to identify criteria that can be used to divide the aggregate population into statistically significant subgroups. By contrast, clustering methods start at the individual level and form segments by aggregating individuals with similar characteristics into groups or segments.
To begin the researcher chooses one or more criteria that will be used to measure similarity between individuals. For segmentation analyses these variables are typically chosen from survey responses or behavioral data. Commonly used survey data includes attitude statements, attribute importance ratings or estimates, brand ratings, and lifestyle or psychographic statements. Individual purchase or usage data may also be used if available. When multiple variables are considered, it may be necessary to standardize them1 so the different variables can receive a comparable weight in measuring similarity between individuals. Care should be exercised in determining the variables to be used in segmentation, often referred to as basis variables, since including variables that do not differentiate among clusters in a meaningful manner causes a serious deterioration in the results of clustering methods. While it is generally not possible to know in advance which variables will differentiate among clusters, the analyst should be able to form a set of behavioral hypotheses that will guide the selection of basis variables.
A second decision concerns the choice type of clustering approach to be used. There are two commonly applied approaches to clustering. In a partition clustering approach, the analyst decides in advance how many clusters should be formed. While computation methodologies vary, a commonly employed procedure will be described intuitively. The first step is to specify “seed” observations are needed, one for each of the desired clusters. The next step is to calculate the distance from each of the remaining observations to each of the seeds and assign each observation to the nearest seed to form an initial set of clusters. Once this initial sorting is completed, the algorithm may terminate if the solution is acceptable or reassign observations among the clusters to produce greater homogeneity within each. A k-means procedure is commonly used to reassign observations. This approach calculates a cluster centroid, which is a point that minimizes the sum of the squared distance between it of each of the observations in the cluster. The centroids for each cluster are then used as new seeds and each observation is reassigned to the centroid to which it is closest. New centroids are calculated and the process continues until further movement of the centroids fails to produce a statistically significant improvement in within cluster homogeneity and between cluster heterogeneity.
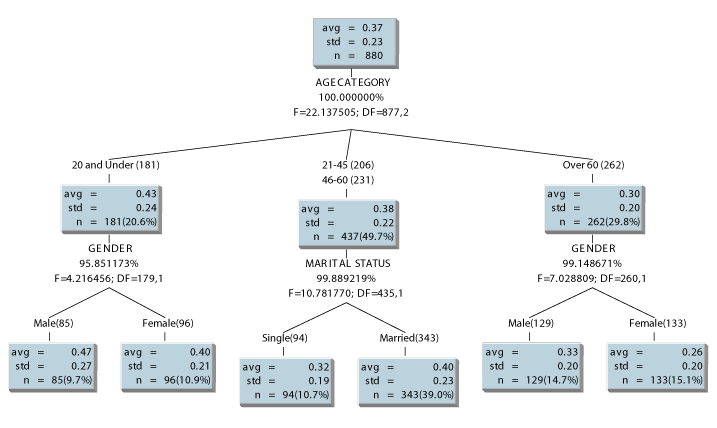
A second approach is known a hierarchical clustering. In this procedure similarity or distance measures are computed between each observation and all others. The clustering process begins by finding the pair of observations that are the most similar to each other in terms of the chosen basis variables and joining them to form a group. The next step is to join the next closest pair of observations and join them or join an existing observation with a previously formed group if the computed distance between the observation and the group is shorter than the distance between any pair of unattached observations.
Figure 2 provides an example that illustrates how groups are formed as a function of distance between observations and groups. In the example, the closest observations are 2 and 9 at a distance of approximately one and they are joined first. Observations 17 and 21 are joined next followed by observations 7 and 11. The next grouping occurs when observation 14 is joined with the group formed by observations 2 and 9. The process continues until all observations are joined in a single group. As can be seen in Figure 2, the results of the clustering process can be depicted in tree-like structures called dendrograms. The analyst chooses number of segments based on the system that proves to be the most useful.
Figure 2. Cluster Analysis Classification Dendrogram
There are several issues that should be considered when undertaking a hierarchical cluster analysis. First is to decide how similarities and differences among observations should be measured. When distances are used typically some form of Minkowski metric is used. The general formula for this type of distance is
![]()
Where,
Dij = the distance between observations i and j
ik and jk = the rating of variable i and j respectively on basis variable k
n = a positive number
The Euclidean distance, which is a Minkowski metric with n equal to 2, is the most commonly used metric. Other commonly used Minkowski metrics are the city block metric (n=1) and the dominance metric that considers only the dimension with the maximum difference (n=8). A correlation coefficient or a measure of matching coefficients (percent of common elements) may be used if similarities between observations are to be used in forming clusters. The appropriate measure depends on the type of variables (interval, binary, or count) used as a basis for clustering analysis and the analysts judgment.
Another design decision concerns how groups should be treated in the clustering process. The single linkage method computes the distance between clusters as the shortest distance between a member of one group and a member of another group. In contrast the complete linkage method computes the distance between clusters as the maximum distance between a member of one group and a member of another group. Average linkage approaches calculate the average distance between the members of one group and the members of the second group. Ward's method is another approach that calculates the total sum of squared deviations from the mean of a cluster and joins clusters that produce the smallest possible increase in the error sum of squares. The choice of linkage rule can have a significant impact on the clusters that are formed. For example, complete linkage clusters tend to be relatively compact and consisting of highly similar observations but may be sensitive to the ordering of data and may yield significantly different results if observations are dropped. In contrast, Single linkage methods yield solutions that are less sensitive to the order of the similarity or distance data but may form long elongated clusters.
Hierarchical clustering methods have the advantage of allowing the analyst to visualize the linkage process and see what observations join at each stage. They also do not require specifying a number of clusters a priori. However, hierarchical methods are more computationally intensive in that distances must be calculated between each pair of points and distances need to be continually recalculated as clusters are formed. Solutions may differ, occasionally dramatically, depending on the similarity/distance measures and linkage methods used. If the analyst is concerned about the stability of the results, the most insightful number of clusters may be determined by a hierarchical analysis and the resulting cluster centroids can be used as seed values for a partition clustering analysis. Another potential limitation of hierarchical cluster analysis is its tendency to form clusters of roughly equal size, even if the underlying population would be expected to have segments with significant differences in size.
Once acceptable clusters are formed, it is important to interpret them in terms of the basis variables. A cross tabular analysis in which one of the categorized variables is cluster membership and the other is a basis variable can reveal systematic deviations in the basis variable across clusters. Similarly an interaction detection analysis, such as CHAID, can identify the correspondence between the clusters and combinations of basis variables that can be used to apply the segmentation scheme to the population as whole.
Segmenting the market is important conducting pricing research since the factors influencing willingness to pay and demand are likely to differ substantially across market segments. It is critical to identify these differences when possible prior to estimating demand and the factors influencing a customer’s willingness to pay. A failure to do so may result in "average" estimates that may apply to none of the market segments which will usually lead to pricing policy mistakes.
